Introduction
In this lecture, we reviewed the definition of the conditional probability with respect to a sub- -field. And then gave several special examples to compute the conditional probability. After mentioning the conditional probability with respect to a random variable, and some function measurability, an easier way to check a conditional probability is given. Finally, we introduce the so-called
-field. And then gave several special examples to compute the conditional probability. After mentioning the conditional probability with respect to a random variable, and some function measurability, an easier way to check a conditional probability is given. Finally, we introduce the so-called 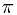 -
-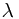 theorem and given an application of it.
theorem and given an application of it.
General Case
Consider the probability measure space 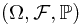 . Event
. Event 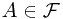 and
and  is a sub-
is a sub- -field. The conditional probability
-field. The conditional probability  satiesfies
satiesfies
-
 is
is  -measurable
-measurable -
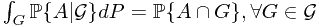 .
.
In the sense of a.e. equal, the random variable is uniquely determined.
These two requirements may seemingly being surprising at the first sight, yet they really have their probabilistic interpretations.
The first entry tells us that by the knowledge of  , we could define
, we could define  .
.
The second entry is understood while determing the price of a gamble. If the expected gain is zero, then the price of entering a gamble must be  . To see this, if
. To see this, if 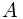 happens, the gain is
happens, the gain is 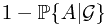 , and if
, and if 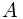 does not happen, the gain will be
does not happen, the gain will be  . Together, the gain will be
. Together, the gain will be

which will lead to the result, if we integral over 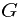 .
.
Ex. What is  if
if 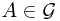 ?
?
Solution. This is Example 33.3. The key is 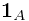 .
.
Ex. What is  if
if 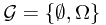 ?
?
Solution. This is Example 33.4. The key is 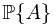 .
.
Ex. Suppose 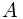 is independent of
is independent of  , i.e.,
, i.e., 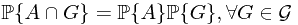 , then what is
, then what is  ?
?
Solution. Intuitively it is 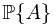 .
.
Ex. Suppose 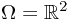 ,
,  ,
, 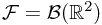 , and
, and
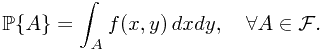
Here, 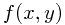 is Borel-measurable functon,
is Borel-measurable functon, 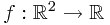 , and
, and  almost everywhere, and
almost everywhere, and 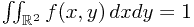 . Countable additivity is trivial to verify. It follows that
. Countable additivity is trivial to verify. It follows that 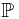 is a probability measure. Suppose
is a probability measure. Suppose  is a sub-
is a sub- -field generated by the form
-field generated by the form 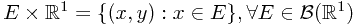 . Let
. Let 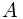 be
be  . What is
. What is  ?
?
Solution. One claims that
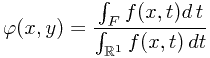
is a version of  . To verify this, one should verify second property of the definition. Since a general element in
. To verify this, one should verify second property of the definition. Since a general element in  takes the form
takes the form 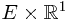 , it is essential to prove that
, it is essential to prove that
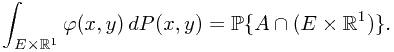
Notice that the right hand side of the equation is exactly 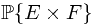 . To evaluate the value on the left hand side, one must resort to the Fubini's Theorem and a previous Theorem.
. To evaluate the value on the left hand side, one must resort to the Fubini's Theorem and a previous Theorem.
It is also possible to define a conditionial probability with respect to random variable 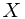 . This could be done by define
. This could be done by define 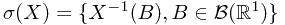 . And define
. And define 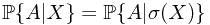 .
.
2024年5月17日 22:14
I really loved reading your blog. It was very well authored and easy to understand..You have a very nice blog. Thank you for sharing..A very awesome blog post. We are really grateful for your blog post. You will find a lot of approaches after visiting your pos
2024年6月12日 19:16
“I have to say, your blog is a breath of fresh air. There are so many generic and uninspired blogs out there, but yours really stands out for its originality and creativity.”
2024年6月12日 19:23
“I have to say, your blog is a breath of fresh air. There are so many generic and uninspired blogs out there, but yours really stands out for its originality and creativity.”
2024年6月12日 19:24
I’m truly enjoying the design and layout of your site. It’s a very easy on the eyes which makes it much more pleasant for me to come here and visit more often. Did you hire out a developer to create your theme? Great work!
2024年6月12日 19:25
I’m truly enjoying the design and layout of your site. It’s a very easy on the eyes which makes it much more pleasant for me to come here and visit more often. Did you hire out a developer to create your theme? Great work!
2024年6月12日 19:26
Great work! That is the kind of info that should be shared across the internet. Shame on Google for now not positioning this submit upper! Come on over and visit my web site . Thanks =)
2024年6月12日 19:26
My spouse and I absolutely love your blog and find a lot of your post’s to be exactly what I’m looking for. Do you offer guest writers to write content in your case? I wouldn’t mind writing a post or elaborating on a few of the subjects you write with regards to here. Again, awesome web site!
2024年6月12日 19:27
This is really likewise an incredibly beneficial placing most of us severely encountered shopping as a result of. It truly is faraway from each and every day we have now possibility to think about something.
2024年6月12日 19:28
I am really enjoying reading your well written articles. It looks like you spend a lot of effort and time on your blog. I have bookmarked it and I am looking forward to reading new articles. Keep up the good work.
2024年6月12日 19:29
Operational Challenges:New Rabbit's continuous address changes may pose inconveniences for users seeking a stable and reliable webtoon experience.
2024年6月12日 21:31
Hi, i feel that i noticed you visited my website so i got here to ?go back the prefer?.I’m trying to to find things to enhance my website!I guess its ok to use some of your ideas!!
2024年6月12日 21:32
Thank you for every other magnificent article. Where else may just anyone get that kind of info in such an ideal manner of writing? I have a presentation subsequent week, and I am at the search for such info.
2024年6月12日 21:33
This is really likewise an incredibly beneficial placing most of us severely encountered shopping as a result of. It truly is faraway from each and every day we have now possibility to think about something.
2024年6月12日 21:34
We’re a group of volunteers and starting a new scheme in our community. Your website provided us with valuable information to work on. You’ve done a formidable job and our entire community will be grateful to you.
2024年6月12日 21:34
I am really enjoying reading your well written articles. It looks like you spend a lot of effort and time on your blog. I have bookmarked it and I am looking forward to reading new articles. Keep up the good work.
2024年6月12日 21:35
Goodness! Such an astounding and supportive post this is. I outrageously cherish it. It's so great thus amazing. I am simply flabbergasted. I trust that you keep on doing your work like this later on moreover.
2024年6月12日 21:35
Great work! That is the kind of info that should be shared across the internet. Shame on Google for now not positioning this submit upper! Come on over and visit my web site . Thanks =)
2024年6月12日 21:37
Awesome article, it was exceptionally helpful! I simply began in this and I'm becoming more acquainted with it better. The post is written in very a good manner and it contains many useful information for me. Thank you very much and will look for more postings from you.
2024年6月12日 21:38
Two full thumbs up for this magneficent article of yours. I've truly delighted in perusing this article today and I figure this may be outstanding amongst other article that I've perused yet. If it's not too much trouble keep this work going ahead in a similar quality.
2024年6月12日 21:44
Goodness! Such an astounding and supportive post this is. I outrageously cherish it. It's so great thus amazing. I am simply flabbergasted. I trust that you keep on doing your work like this later on moreover.
2024年6月12日 21:47
This is really likewise an incredibly beneficial placing most of us severely encountered shopping as a result of. It truly is faraway from each and every day we have now possibility to think about something.
2024年6月12日 21:48
Oh my goodness! an amazing article dude. Thank you Nonetheless I’m experiencing concern with ur rss . Don?t know why Unable to subscribe to it. Is there anybody getting equivalent rss problem? Anyone who is aware of kindly respond. Thnkx
2024年6月12日 21:49
I appreciated how flexible the team at amcauto.co was when it came to scheduling appointments and test drives. They were always willing to work around my schedule.
2024年6月12日 21:49
“I have to say, your blog is a breath of fresh air. There are so many generic and uninspired blogs out there, but yours really stands out for its originality and creativity.”
2024年6月12日 21:50
Hello, you used to write excellent, but the last few posts have been kinda boring? I miss your tremendous writings. Past several posts are just a little out of track! come on!
2024年6月12日 21:51
I’m not that much of a internet reader to be honest but your blogs really nice, keep it up! I’ll go ahead and bookmark your site to come back down the road. Cheers
2024年6月12日 21:52
I was suggested this web site through my cousin. I’m not certain whether this put up is written through him as no one else recognize such exact approximately my difficulty. You’re wonderful! Thank you!
2024年6月12日 21:52
Hello, you used to write excellent, but the last few posts have been kinda boring? I miss your tremendous writings. Past several posts are just a little out of track! come on!
2024年6月12日 21:54
I’m not that much of a internet reader to be honest but your blogs really nice, keep it up! I’ll go ahead and bookmark your site to come back down the road. Cheers