In this lecture note, we are going to discuss 7 topics, which is outlined as follows:
-
Conditioned Expectation
-
Discrete-Time Martingale
-
Continuous-Time Martingale
-
Stochastic Integral
-
Strong Solution of SDE
-
Weak Solution of SDE (optional)
-
Applications (optional)
References
-
Steven E. Shreve and Ioannis Karatres, Brownian Motion and Stochastic Calculus
-
Rick Durret, Probability: Theory and Examples
-
Patrick Billingslay: Probability and Measure
Topic 1: Conditioned Probability, Distribution and Expectations
Let 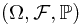 be a probability measure space, and
be a probability measure space, and 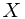 be a random variable. Actually,
be a random variable. Actually, 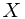 is a functional from
is a functional from 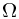 to
to 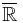 satisfying that for all
satisfying that for all 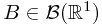 ,
,
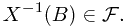
This means every pre-image of a Borel set in the real number is in the  -algebra.
-algebra.
Mathematical expectation is defined by
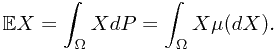
where 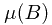 represents the probability of the preimage of Borel set
represents the probability of the preimage of Borel set 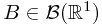 , i.e.,
, i.e.,
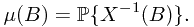
Ex: Prove that 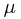 is a measure on
is a measure on 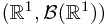 .
.
Proof. Let us write the definition of a measure. The following is copied from Wikipedia measure (mathematics). If 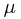 is a measure, three conditions must hold, i.e.,
is a measure, three conditions must hold, i.e.,
Let  be a
be a  -algebra over
-algebra over 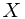 , a function
, a function 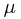 from
from  to the extended real number line is called a measure, if it satisfies the following properties:
to the extended real number line is called a measure, if it satisfies the following properties:
-
Non-negativity
-
Null empty set
-
Countable additivity
First of all, 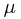 is a set function from
is a set function from  to
to ![$[0, 1]$ $[0, 1]$](http://davidguqun.is-programmer.com/user_files/davidguqun/epics/54a448dbbad7d82a6d7e1d03d2ec39300d9a4ab4.png) . Non-negativity follows from the non-negativity of
. Non-negativity follows from the non-negativity of 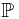 . To see the null empty set property, we check that if
. To see the null empty set property, we check that if 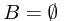 implies that
implies that 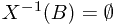 . By the null empty set property of
. By the null empty set property of 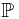 , we arrive at the null empty set property of
, we arrive at the null empty set property of 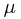 . And finally, for countable additivity, suppose
. And finally, for countable additivity, suppose 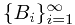 are disjoint sets in
are disjoint sets in  , then by the definition of
, then by the definition of 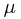 , we have
, we have
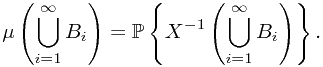
By the operation of set, and the disjointness of 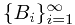 we have
we have
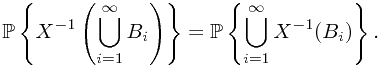
and finally by the countable additivity, we have
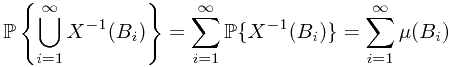
which arrive at the conclusion that satisfy countable additivity.
1.1 Sub- -field and Information
-field and Information
In this subsection, an heuristic example is provided to explain the meaning of a sub- -field. In general cases, a sub-
-field. In general cases, a sub- -field could be approximatedly understood as information.
-field could be approximatedly understood as information.
Example: [Toss of a coin 3 times]
All the possible out come constructs the sample space 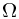 , which takes the form
, which takes the form
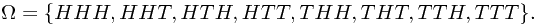
After first toss, the sample space could be divided into two parts, as 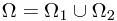 , where
, where
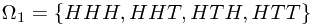 , and
, and 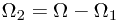 .
.
We can consider the corresponding  -algebra:
-algebra: 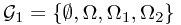 , which stands for the ``information'' after the first toss. When a sample
, which stands for the ``information'' after the first toss. When a sample 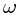 is given, whose first experiment is a head, we can tell that
is given, whose first experiment is a head, we can tell that  is not in
is not in 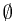 ,
, 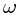 is in
is in 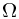 ,
, 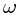 is in
is in 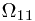 and
and 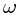 is not in
is not in 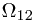 . And look it in another angle, we see that, this
. And look it in another angle, we see that, this  -algebra contains all the possible situations for different ``first toss'' cases.
-algebra contains all the possible situations for different ``first toss'' cases.
It is quite easy to generalize to the ``information''  -field after second toss
-field after second toss 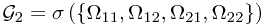 .
.
Generally speaking, if  is a sub-
is a sub- -field of
-field of 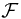 , the information of
, the information of  is understood as
is understood as
for all 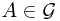 , one know whether
, one know whether 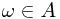 or not. In other word, the indicator function is well-defined
or not. In other word, the indicator function is well-defined 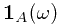 .
.
1.2 Conditional Probability
In this subsection, a theoretical treatment of conditional probability is concerned. As we know in the elementary probability theory, the nature definition for conditional probability is govened by the following equation
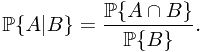
Therefore, it is natural to raise the question how to define  , where
, where  is a sub-
is a sub- -field?
-field?
Note: The lecture notes follows majorly from reference book 3---Patrick Billingsley's Probability and Measure, Section 33.
Sometimes,  is quite complicated. Thus, instead, we consider the simple case when
is quite complicated. Thus, instead, we consider the simple case when  is generated by some disjoint
is generated by some disjoint 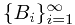 instead, where
instead, where 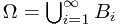 . Therefore, we have
. Therefore, we have 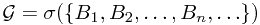 .
.
Then  can be defined pathwisely, by
can be defined pathwisely, by
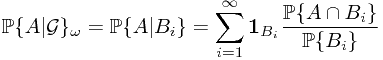
for all sample 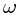 in sample space
in sample space 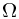 .
.
Before we goto see the formal definition, we examine an example, which comes from the problem of predicting the telephone call probability.
Example: [Apply Simple Case to Computing Conditional Probability]
Consider a Poisson process  on measure space
on measure space 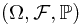 . Let
. Let 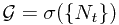 and
and 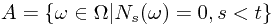 . Compute
. Compute  .
.
Solution. Recall some of the knowledge of Poisson process now. By Wikipedia Poisson Process, we have
-
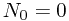
-
Independent increments
-
Stationary increments
-
No counted occurrences are simultaneous
The result of this defintion is that  where
where 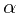 is the intensity.
is the intensity.
Note: If 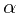 is a constant, this is the case of homogeneous Poisson process, which is also named as Lévy processes.
is a constant, this is the case of homogeneous Poisson process, which is also named as Lévy processes.
It follows that
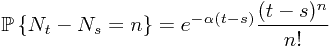
for all 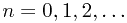 and
and 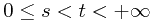 .
.
Another explaination is also need for 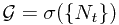 . This is a sigma field
. This is a sigma field
Now, let  . Obviously, the union of all these set is the sample space
. Obviously, the union of all these set is the sample space 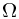 . Moreover, they are obviously disjoint. Then by the computation formula in the simple case, we have
. Moreover, they are obviously disjoint. Then by the computation formula in the simple case, we have
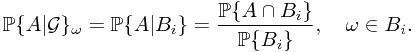
To compute 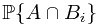 and
and  , we have
, we have
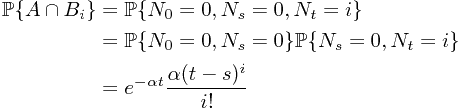
and
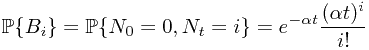
which gives rise to the final result
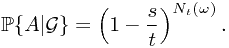
Ex. Prove that  is
is  -measurable;
-measurable;
Proof. Recall the definition of  -measurable. If a random variable
-measurable. If a random variable 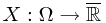 is
is  -measurable, then for all
-measurable, then for all 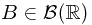 , we have its pre-image
, we have its pre-image 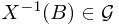 . Or equivalently,
. Or equivalently, 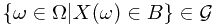 . In this case, we are going to prove that
. In this case, we are going to prove that 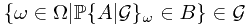 . It reduced to the problem that
. It reduced to the problem that 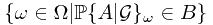 could be written as some union of
could be written as some union of 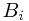 ?
?
Since for all  ,
,  is a constant.
is a constant.
Ex. Prove that 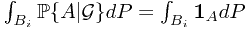 holds.
holds.
Proof. Note that the left hand side equals to  which is identical with the right hand side.
which is identical with the right hand side.
Now we go further to the general cases for  . Suppose,
. Suppose, 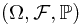 is a probability measure space,
is a probability measure space,  is a sub-
is a sub- -field, event
-field, event 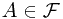 . Then, we claim the conditional probability of
. Then, we claim the conditional probability of 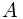 given
given  is a random variable satisfying (1)
is a random variable satisfying (1)  is
is  -measurable; (2)
-measurable; (2) 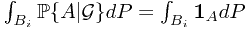 . The random variable exists and unique, by Radon-Nikodym Theorem.
. The random variable exists and unique, by Radon-Nikodym Theorem.
Let 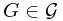 and
and 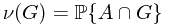
Ex. Prove that 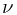 is a measure on
is a measure on  .
.
Proof. 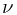 is a function that
is a function that ![$\nu: \mathcal G \to [0, 1]$ $\nu: \mathcal G \to [0, 1]$](http://davidguqun.is-programmer.com/user_files/davidguqun/epics/d6cb51681ee82ade4c82a4059f2662d777a40d23.png) . Non-negative property and emptyset property are trivial. Countable additivity follows from the countable additivity of probability measure
. Non-negative property and emptyset property are trivial. Countable additivity follows from the countable additivity of probability measure 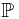 .
.
Ex. Prove that 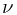 is absolute continuous with respect to
is absolute continuous with respect to 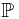 on
on  .
.
Proof. By Wikipedia, absolute continuity, we know that if 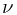 is absolute continuous with respect to
is absolute continuous with respect to 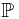 on
on  , this means that for all
, this means that for all 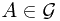 and
and 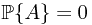 implies that
implies that  . This is obvious, since
. This is obvious, since 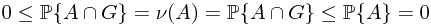 .
.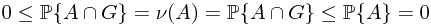 ..
..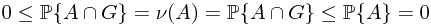
Ex. If 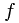 and
and 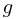 are
are  -measurable, and
-measurable, and 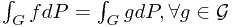 , then
, then 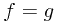 almost surely.
almost surely.
Proof.
 -field. And then gave several special examples to compute the conditional probability. After mentioning the conditional probability with respect to a random variable, and some function measurability, an easier way to check a conditional probability is given. Finally, we introduce the so-called
-field. And then gave several special examples to compute the conditional probability. After mentioning the conditional probability with respect to a random variable, and some function measurability, an easier way to check a conditional probability is given. Finally, we introduce the so-called 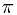 -
-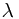 theorem and given an application of it.
theorem and given an application of it.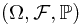 . Event
. Event 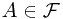 and
and  is a sub-
is a sub- -field. The conditional probability
-field. The conditional probability  satiesfies
satiesfies is
is  -measurable
-measurable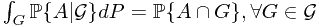 .
. , we could define
, we could define  .
. . To see this, if
. To see this, if 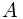 happens, the gain is
happens, the gain is 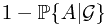 , and if
, and if 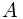 does not happen, the gain will be
does not happen, the gain will be  . Together, the gain will be
. Together, the gain will be
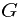 .
. if
if 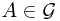 ?
?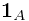 .
. if
if 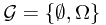 ?
?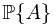 .
.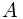 is independent of
is independent of  , i.e.,
, i.e., 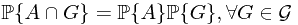 , then what is
, then what is  ?
?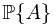 .
.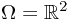 ,
,  ,
, 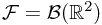 , and
, and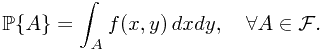
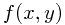 is Borel-measurable functon,
is Borel-measurable functon, 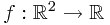 , and
, and  almost everywhere, and
almost everywhere, and 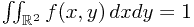 . Countable additivity is trivial to verify. It follows that
. Countable additivity is trivial to verify. It follows that 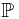 is a probability measure. Suppose
is a probability measure. Suppose  is a sub-
is a sub- -field generated by the form
-field generated by the form 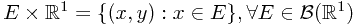 . Let
. Let 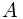 be
be  . What is
. What is  ?
?
 . To verify this, one should verify second property of the definition. Since a general element in
. To verify this, one should verify second property of the definition. Since a general element in  takes the form
takes the form 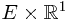 , it is essential to prove that
, it is essential to prove that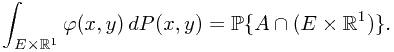
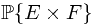 . To evaluate the value on the left hand side, one must resort to the Fubini's Theorem and a previous Theorem.
. To evaluate the value on the left hand side, one must resort to the Fubini's Theorem and a previous Theorem.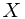 . This could be done by define
. This could be done by define 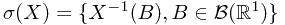 . And define
. And define 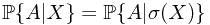 .
.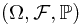 be a probability measure space, and
be a probability measure space, and 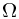 to
to 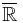 satisfying that for all
satisfying that for all 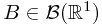 ,
,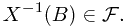
 -algebra.
-algebra.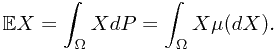
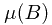 represents the probability of the preimage of Borel set
represents the probability of the preimage of Borel set 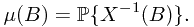
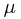 is a measure on
is a measure on 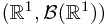 .
. be a
be a  to
to ![$[0, 1]$ $[0, 1]$](http://davidguqun.is-programmer.com/user_files/davidguqun/epics/54a448dbbad7d82a6d7e1d03d2ec39300d9a4ab4.png) . Non-negativity follows from the non-negativity of
. Non-negativity follows from the non-negativity of 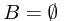 implies that
implies that 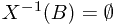 . By the null empty set property of
. By the null empty set property of 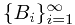 are disjoint sets in
are disjoint sets in 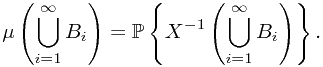
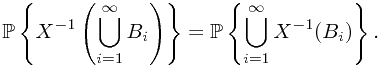
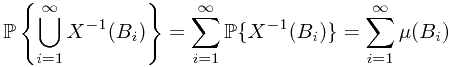
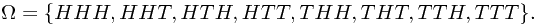
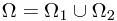 , where
, where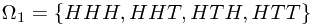 , and
, and 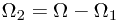 .
.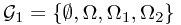 , which stands for the ``information'' after the first toss. When a sample
, which stands for the ``information'' after the first toss. When a sample 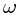 is given, whose first experiment is a head, we can tell that
is given, whose first experiment is a head, we can tell that 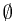 ,
, 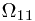 and
and 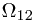 . And look it in another angle, we see that, this
. And look it in another angle, we see that, this 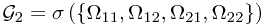 .
. is a sub-
is a sub-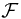 , the information of
, the information of 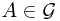 , one know whether
, one know whether 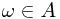 or not. In other word, the indicator function is well-defined
or not. In other word, the indicator function is well-defined 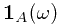 .
.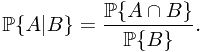
 , where
, where 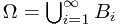 . Therefore, we have
. Therefore, we have 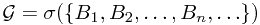 .
.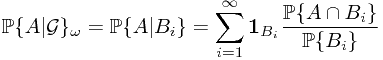
 on measure space
on measure space 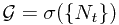 and
and 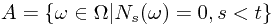 . Compute
. Compute 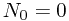
 where
where 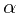 is the intensity.
is the intensity.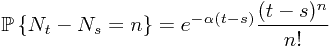
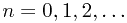 and
and 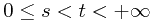 .
. . Obviously, the union of all these set is the sample space
. Obviously, the union of all these set is the sample space 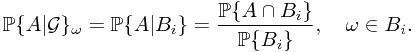
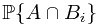 and
and  , we have
, we have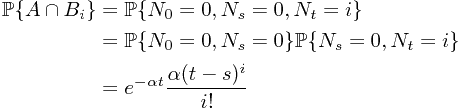
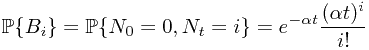
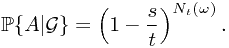
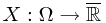 is
is 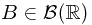 , we have its pre-image
, we have its pre-image 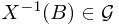 . Or equivalently,
. Or equivalently, 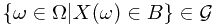 . In this case, we are going to prove that
. In this case, we are going to prove that 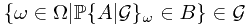 . It reduced to the problem that
. It reduced to the problem that 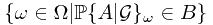 could be written as some union of
could be written as some union of 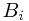
 ,
, 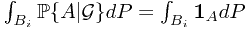 holds.
holds. which is identical with the right hand side.
which is identical with the right hand side.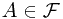 . Then, we claim the conditional probability of
. Then, we claim the conditional probability of 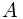 given
given 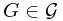 and
and 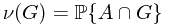
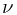 is a measure on
is a measure on  .
.![$\nu: \mathcal G \to [0, 1]$ $\nu: \mathcal G \to [0, 1]$](http://davidguqun.is-programmer.com/user_files/davidguqun/epics/d6cb51681ee82ade4c82a4059f2662d777a40d23.png) . Non-negative property and emptyset property are trivial. Countable additivity follows from the countable additivity of probability measure
. Non-negative property and emptyset property are trivial. Countable additivity follows from the countable additivity of probability measure 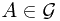 and
and 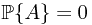 implies that
implies that  . This is obvious, since
. This is obvious, since 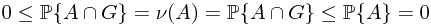 .
.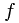 and
and 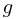 are
are 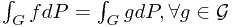 , then
, then 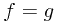 almost surely.
almost surely.