Let me start with a test for TeX:
[tex]$-{\hbar^2 \over 2m}$[\tex]
Introduction
In this lecture, we reviewed the definition of the conditional probability with respect to a sub- -field. And then gave several special examples to compute the conditional probability. After mentioning the conditional probability with respect to a random variable, and some function measurability, an easier way to check a conditional probability is given. Finally, we introduce the so-called
-field. And then gave several special examples to compute the conditional probability. After mentioning the conditional probability with respect to a random variable, and some function measurability, an easier way to check a conditional probability is given. Finally, we introduce the so-called 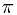 -
-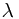 theorem and given an application of it.
theorem and given an application of it.
General Case
Consider the probability measure space 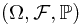 . Event
. Event 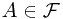 and
and  is a sub-
is a sub- -field. The conditional probability
-field. The conditional probability  satiesfies
satiesfies
 is
is  -measurable
-measurable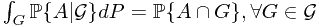 .
.In the sense of a.e. equal, the random variable is uniquely determined.
These two requirements may seemingly being surprising at the first sight, yet they really have their probabilistic interpretations.
The first entry tells us that by the knowledge of  , we could define
, we could define  .
.
The second entry is understood while determing the price of a gamble. If the expected gain is zero, then the price of entering a gamble must be  . To see this, if
. To see this, if 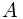 happens, the gain is
happens, the gain is 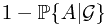 , and if
, and if 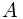 does not happen, the gain will be
does not happen, the gain will be  . Together, the gain will be
. Together, the gain will be

which will lead to the result, if we integral over 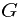 .
.
Ex. What is  if
if 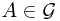 ?
?
Solution. This is Example 33.3. The key is 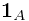 .
.
Ex. What is  if
if 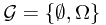 ?
?
Solution. This is Example 33.4. The key is 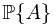 .
.
Ex. Suppose 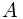 is independent of
is independent of  , i.e.,
, i.e., 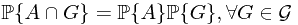 , then what is
, then what is  ?
?
Solution. Intuitively it is 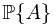 .
.
Ex. Suppose 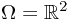 ,
,  ,
, 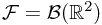 , and
, and
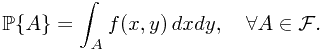
Here, 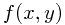 is Borel-measurable functon,
is Borel-measurable functon, 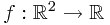 , and
, and  almost everywhere, and
almost everywhere, and 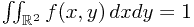 . Countable additivity is trivial to verify. It follows that
. Countable additivity is trivial to verify. It follows that 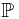 is a probability measure. Suppose
is a probability measure. Suppose  is a sub-
is a sub- -field generated by the form
-field generated by the form 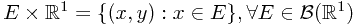 . Let
. Let 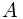 be
be  . What is
. What is  ?
?
Solution. One claims that
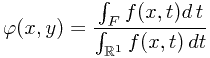
is a version of  . To verify this, one should verify second property of the definition. Since a general element in
. To verify this, one should verify second property of the definition. Since a general element in  takes the form
takes the form 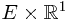 , it is essential to prove that
, it is essential to prove that
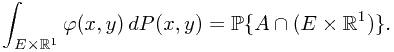
Notice that the right hand side of the equation is exactly 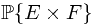 . To evaluate the value on the left hand side, one must resort to the Fubini's Theorem and a previous Theorem.
. To evaluate the value on the left hand side, one must resort to the Fubini's Theorem and a previous Theorem.
It is also possible to define a conditionial probability with respect to random variable 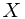 . This could be done by define
. This could be done by define 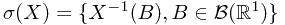 . And define
. And define 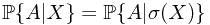 .
.
In this lecture note, we are going to discuss 7 topics, which is outlined as follows:
References
Topic 1: Conditioned Probability, Distribution and Expectations
Let 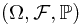 be a probability measure space, and
be a probability measure space, and 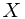 be a random variable. Actually,
be a random variable. Actually, 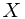 is a functional from
is a functional from 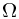 to
to 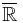 satisfying that for all
satisfying that for all 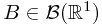 ,
,
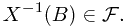
This means every pre-image of a Borel set in the real number is in the  -algebra.
-algebra.
Mathematical expectation is defined by
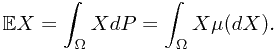
where 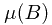 represents the probability of the preimage of Borel set
represents the probability of the preimage of Borel set 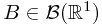 , i.e.,
, i.e.,
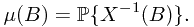
Ex: Prove that 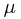 is a measure on
is a measure on 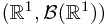 .
.
Proof. Let us write the definition of a measure. The following is copied from Wikipedia measure (mathematics). If 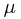 is a measure, three conditions must hold, i.e.,
is a measure, three conditions must hold, i.e.,
Let  be a
be a  -algebra over
-algebra over 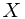 , a function
, a function 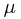 from
from  to the extended real number line is called a measure, if it satisfies the following properties:
to the extended real number line is called a measure, if it satisfies the following properties:
First of all, 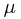 is a set function from
is a set function from  to
to ![$[0, 1]$ $[0, 1]$](http://davidguqun.is-programmer.com/user_files/davidguqun/epics/54a448dbbad7d82a6d7e1d03d2ec39300d9a4ab4.png) . Non-negativity follows from the non-negativity of
. Non-negativity follows from the non-negativity of 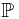 . To see the null empty set property, we check that if
. To see the null empty set property, we check that if 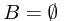 implies that
implies that 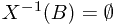 . By the null empty set property of
. By the null empty set property of 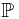 , we arrive at the null empty set property of
, we arrive at the null empty set property of 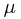 . And finally, for countable additivity, suppose
. And finally, for countable additivity, suppose 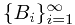 are disjoint sets in
are disjoint sets in  , then by the definition of
, then by the definition of 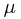 , we have
, we have
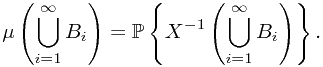
By the operation of set, and the disjointness of 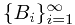 we have
we have
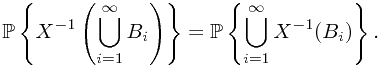
and finally by the countable additivity, we have
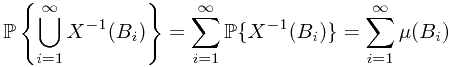
which arrive at the conclusion that satisfy countable additivity.
1.1 Sub- -field and Information
-field and Information
In this subsection, an heuristic example is provided to explain the meaning of a sub- -field. In general cases, a sub-
-field. In general cases, a sub- -field could be approximatedly understood as information.
-field could be approximatedly understood as information.
Example: [Toss of a coin 3 times]
All the possible out come constructs the sample space 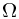 , which takes the form
, which takes the form
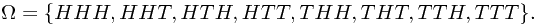
After first toss, the sample space could be divided into two parts, as 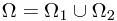 , where
, where
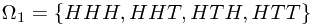 , and
, and 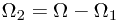 .
.
We can consider the corresponding  -algebra:
-algebra: 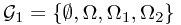 , which stands for the ``information'' after the first toss. When a sample
, which stands for the ``information'' after the first toss. When a sample 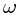 is given, whose first experiment is a head, we can tell that
is given, whose first experiment is a head, we can tell that 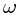 is not in
is not in 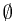 ,
, 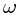 is in
is in 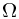 ,
, 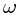 is in
is in 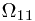 and
and 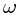 is not in
is not in 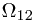 . And look it in another angle, we see that, this
. And look it in another angle, we see that, this  -algebra contains all the possible situations for different ``first toss'' cases.
-algebra contains all the possible situations for different ``first toss'' cases.
It is quite easy to generalize to the ``information''  -field after second toss
-field after second toss 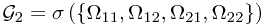 .
.
Generally speaking, if  is a sub-
is a sub- -field of
-field of 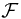 , the information of
, the information of  is understood as
is understood as
for all 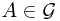 , one know whether
, one know whether 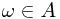 or not. In other word, the indicator function is well-defined
or not. In other word, the indicator function is well-defined 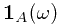 .
.
1.2 Conditional Probability
In this subsection, a theoretical treatment of conditional probability is concerned. As we know in the elementary probability theory, the nature definition for conditional probability is govened by the following equation
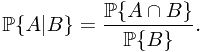
Therefore, it is natural to raise the question how to define  , where
, where  is a sub-
is a sub- -field?
-field?
Note: The lecture notes follows majorly from reference book 3---Patrick Billingsley's Probability and Measure, Section 33.
Sometimes,  is quite complicated. Thus, instead, we consider the simple case when
is quite complicated. Thus, instead, we consider the simple case when  is generated by some disjoint
is generated by some disjoint 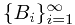 instead, where
instead, where 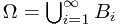 . Therefore, we have
. Therefore, we have 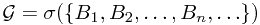 .
.
Then  can be defined pathwisely, by
can be defined pathwisely, by
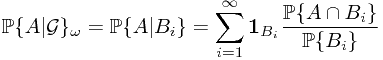
for all sample 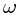 in sample space
in sample space 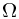 .
.
Before we goto see the formal definition, we examine an example, which comes from the problem of predicting the telephone call probability.
Example: [Apply Simple Case to Computing Conditional Probability]
Consider a Poisson process  on measure space
on measure space 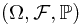 . Let
. Let 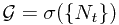 and
and 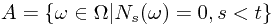 . Compute
. Compute  .
.
Solution. Recall some of the knowledge of Poisson process now. By Wikipedia Poisson Process, we have
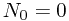
The result of this defintion is that  where
where 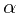 is the intensity.
is the intensity.
Note: If 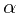 is a constant, this is the case of homogeneous Poisson process, which is also named as Lévy processes.
is a constant, this is the case of homogeneous Poisson process, which is also named as Lévy processes.
It follows that
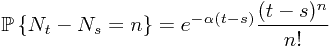
for all 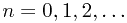 and
and 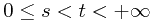 .
.
Another explaination is also need for 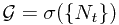 . This is a sigma field
. This is a sigma field
Now, let  . Obviously, the union of all these set is the sample space
. Obviously, the union of all these set is the sample space 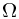 . Moreover, they are obviously disjoint. Then by the computation formula in the simple case, we have
. Moreover, they are obviously disjoint. Then by the computation formula in the simple case, we have
To compute  and
and  , we have
, we have
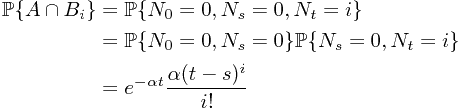
and
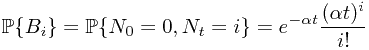
which gives rise to the final result
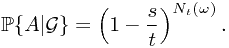
Ex. Prove that  is
is  -measurable;
-measurable;
Proof. Recall the definition of  -measurable. If a random variable
-measurable. If a random variable 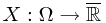 is
is  -measurable, then for all
-measurable, then for all 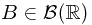 , we have its pre-image
, we have its pre-image 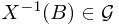 . Or equivalently,
. Or equivalently, 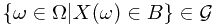 . In this case, we are going to prove that
. In this case, we are going to prove that 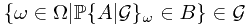 . It reduced to the problem that
. It reduced to the problem that 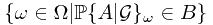 could be written as some union of
could be written as some union of 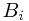 ?
?
Since for all  ,
,  is a constant.
is a constant.
Ex. Prove that 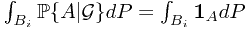 holds.
holds.
Proof. Note that the left hand side equals to  which is identical with the right hand side.
which is identical with the right hand side.
Now we go further to the general cases for  . Suppose,
. Suppose, 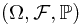 is a probability measure space,
is a probability measure space,  is a sub-
is a sub- -field, event
-field, event 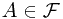 . Then, we claim the conditional probability of
. Then, we claim the conditional probability of 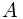 given
given  is a random variable satisfying (1)
is a random variable satisfying (1)  is
is  -measurable; (2)
-measurable; (2) 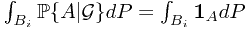 . The random variable exists and unique, by Radon-Nikodym Theorem.
. The random variable exists and unique, by Radon-Nikodym Theorem.
Let 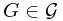 and
and 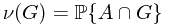
Ex. Prove that 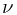 is a measure on
is a measure on  .
.
Proof. 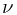 is a function that
is a function that ![$\nu: \mathcal G \to [0, 1]$ $\nu: \mathcal G \to [0, 1]$](http://davidguqun.is-programmer.com/user_files/davidguqun/epics/d6cb51681ee82ade4c82a4059f2662d777a40d23.png) . Non-negative property and emptyset property are trivial. Countable additivity follows from the countable additivity of probability measure
. Non-negative property and emptyset property are trivial. Countable additivity follows from the countable additivity of probability measure 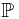 .
.
Ex. Prove that 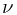 is absolute continuous with respect to
is absolute continuous with respect to 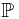 on
on  .
.
Proof. By Wikipedia, absolute continuity, we know that if 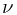 is absolute continuous with respect to
is absolute continuous with respect to 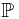 on
on  , this means that for all
, this means that for all 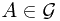 and
and 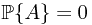 implies that
implies that  . This is obvious, since
. This is obvious, since 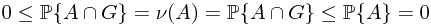 .
.
Ex. If 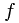 and
and 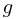 are
are  -measurable, and
-measurable, and 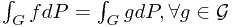 , then
, then 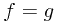 almost surely.
almost surely.
Proof.
To day, I'd like to begin my journey of blogging my PhD. study life in Fudan university, as a member of Computational Mathematics direction.
For a student of computational mathematics, one has to find his/her academic background. In Fudan University, a lot of professors are entitled with computational PhD. As my current boss, Professor Weiguo Gao, he is interested in electronic structure calculations, and numerical problems in network and control flows. As Professor Yangfeng Su, the computations in Very-Large-Scale-Integrationi (VLSI). As Professor Jungong Xue puts his effort in stochastic problems. All of them have a deep understanding in numerical linear algebra and related algorithms, as well as having a basic understanding of the background they are going to deal with. Last month, due to the application of CSC Program, I have got a chance to work with Carlos Javier Garcia-Cervera. And I got the invitation letter. The research is entitled with ``First principle calculations of Continuous Solvent''. I think it is a very good starting point to open my career of doing research.
So far as I know, computational physics, chemistry, or even biology is a hot research field all over the world. Take computational physics an example, people are eager to know what solid behaves. A number of questions could be raised. What is their permittivity? How to compute their heat conductivity? Which color will the look like? How to predict the magnetic behavior of a iron? Of course, there are a lot of work had been done and the theory is also well established.
What can I do? Maybe I should go to do a search of articles that already exist about the continuous solvent. In period one, I think the very first paper I should read is written by Professor Weiguo Gao and Professor Zhipan Liu. The second step is to guess out what Professor Carlos would like to view the problem. The third step is to read some of the publication of Professor Weinan E to see what was going on. In period two, I would like to do a review on the numerical methods that exists for continuous solvents.
Ah, I need to make friends with Wei Wang and Weile Jia from Beijing USTC. It is pretty strange that I can not find any information about them on Google. Nah, forget it.
Ah, I also want to have a talk with Snoozy Liu tomorrow. When will she go to the office? I have to take care of her. And next, I am going to discuss with her future, which is quite an impossible problem at the first sight, yet we have to get an answer. Yes, just as the Social Network tells us, the further is unpredictable. Yes, she is on duty tomorrow, but is not sure when she will arrive. Therefore, we can have a talk maybe around noon. In my opinion, I should respect her idea of her life. As a boyfriend, I should give her suggestion on what is worthy to be done or what is not. But the decision right is her. So the next question is that what is my idea about her career? She wants to be a what? As a faculty? As a staff working in the bank? Yes, probably, she only got two answers listed above. And she might agree that she wants to become a faculty more than a staff, I bet. To become a Professor, one has to have something that he/she is not replaceable. How to demonstrate that you are the exclusive one? The factors we can control: according to your career path, according to the paper you published. My conclusion will be that it is a good experience of study over sea. But is it worthy to quit from Fudan to apply for the US school? I should listen to her motivation! If the motivation is right, then, I should give a supportive attitude and will encourage her to fulfill her career. Yes! A wise solution exists that she could prepare the English tests first to consider more on her career path.
The real work we are going to do now is sure, to get a firm basic of knowledge for the future. She might agree to take a TOEFL and a GRE test this year. Usually it will cost her 3 months to prepare TOEFL and half a year of preparing GRE. Here comes the question, whether it is a good idea to go to France? Learning a completely new language is surely a time-consuming task. It has already been too full for her to get the mathematics right and the English good! So, I don't think so. Maybe its a good idea to postpone studying French to the first year of graduate school. I should ask Yingxing Zhao or Zhenjie Ren for advices. Therefore, preparing TOEFL test will be the Task No. 1. Preparing GRE will be the Task No. 2. Preparing French will be the Task No. 3. And I will not enourage her for getting a job now, since she had already decided to get a PhD in Fudan.
OK, back to my career, I should now do three tasks in the next 24 hours.
First one, finish the C code for B variation of GMRES.
Two, get matrices from FEMLAB.
Three, do all experiments.
Have a nice night~!
Host by is-Programmer.com | Power by Chito 1.3.3 beta | Theme: Aeros 2.0 by TheBuckmaker.com